Úkol č. 11

Elasticita, včetně paradoxu velké úrody atd.

Příklady k postupnému procvičování

• Zvol funkci rostoucí, resp. klesající a urči graficky jejich elasticity (viz přednáškové slidy).
• Zvol funkci nabídky (kvadratickou) a urči její elasticitu jako funkci, pak v jednom bodě - početně, graficky (viz příklad ze cvičení).
• Skupinový příklad pro změny diskrétní (pro poslední dodatečnou jednotku, viz Vaše ekonomické příklady, např. o snižování cen letenek apod.) - jen pro zájemce (nemusíte).
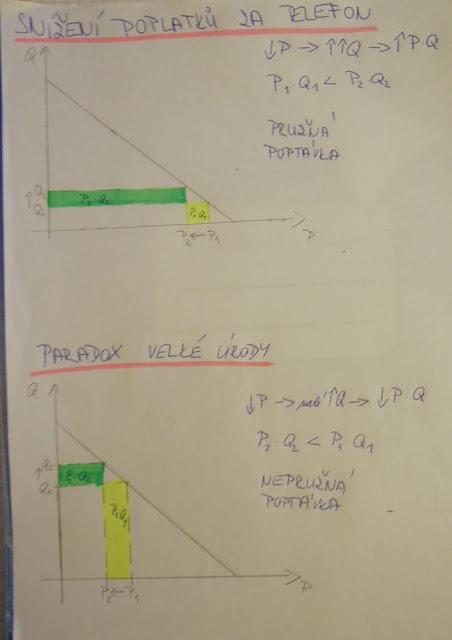
• Paradox velké úrody, resp. snížení poplatků za telefon (velmi často bývá na písemkách)!!!

Úkol č. 9

Vztah mezi veličinami průměrnými a mezními

 - Diskuze našeho týmu k tématu:

Příspěvky ve fóru:
 - Magda:

Ahoj týme,
můžete si zkusit tipnout, který z grafů mezních veličin je správně:-).

https://docs.google.com/file/d/0B90Ik4HFF4sMRTRMV29zay1TeVNYY1VoRkRIQWxhUQ/edit

 - Já:

Ahoj, nechybí ti tam ještě možnost d) ? :D
Když funkci y=(x+2)²+1 zderivuju tak mi vyjde y´=2x+4 - teda alespoň podle mě :) takže tím pádem mi vychází jiná funkce než tam máš nakreslenou (začíná od 4 a má rychlost 2)..
Možná si to všechno myslím špatně - dívala jsem se na to do repository a pochopila jsem to takhle..
Ale možná to všechno chápu špatně :)

  - Magda:

Ona vychází z 4 s rychlostí 2, jenom ty moje obrázky zachycují protažení toho grafu mezní veličiny na druhou stranu, takže by toi mělo být a). Myslím:-).

 - Já

Jo aha už to vidím.. Vůbec mi nedošlo jak vypadá na druhé straně a zmátlo mě, že tam nemáš to protnutí osy y ve 4 :) já jsem si to kreslila nějak takhle (viz níže uvedený obrázek) - dokreslila jsem tam i druhou stranu :-) tím pádem se to shoduje s odpovědí a)

Úkol č. 8

Maximalizace zisku

• Výpočtem hledejte maximální zisk pomocí dvou metod:
  
• MC = MR (ekonomické pravidlo)
• Hledání extrému funkce (využití diferenciálního počtu)
• a hledejte spojitosti obou výpočtů.
• Zakreslete pod sebe 3 související grafy a do nich VŠECHNY RELEVANTNÍ ÚDAJE A SOUVISLOSTI (POPIŠTE CO NEJVÍCE):
• TR, TC
• MR, MC
• zisk pi
• Hledejte pro funkce:
• TR = 11 300 Q - 22Q²
• TC = 4 Q³ - 16 Q² + 140 Q + 1780

• Pro nákresy určujte vrcholy, resp. konvexnost a konkávnost funkcí aj.

                                                                                                                                                                 

 Řešení: 

Z výše uvedeného můžeme vyčíst, že nejvyšší zisk je při Q=30 a to 219 620,- Kč.

Úkol č. 6

Hladká funkce

• Pochopte prostý pojem HLADKOST, pak jej dokážete vysvětlit exaktně. Cvičte si přesné vyjadřování, vše doplňujte vysvětlováním na obrázcích. Inspirací Vám může být studijní materiál z Repository s názvem Hladká funkce.

 V řešení tohoto úkolu se ověřovala hypotéza, která tvrdila, že je křivka hladká. Dále se ověřovalo nepotvrzení této hypotézy zjišťováním, zda je fce spojitá.

Úkol č. 5

Mezní sklon ke spotřebě

• Rozumím tomu, proč mezní sklon ke spotřebě nabývá hodnot mezi nulou a jedničkou, nebo jsem se tuto skutečnost jen naučil(a)? Popište své znalosti o tom, proč tomu tak je. Nemusíte všechno vymyslet sami, využijte dostupné zdroje - tím, že si informace vlastnoručně (a zejména "vlastnohlavně" :-)) zapíšete, mnohé si uvědomíte a pochopíte, také lépe zapamatujete. 
• Možná můžete začít tím, že vložíte odkaz na studijní materiál, který se tímto zabývá a je součástí tohoto kurzu - najdete jej v repository. Už jste jej našli? Vložte odkaz pro ostatní. Pak s ním pracujte, zapisujte si a některé své pěkné výstupy ukažte - zde prostřednictvím fóra - svým kolegům!

Z výše uvedeného můžeme vidět jednotlivé souvislosti mezi spotřební funkcí a mezním sklonem ke spotřebě. Lze pochopit, že mezní sklon ke spotřebě udává rychlost změn spotřební funkce při rostoucím důchodu.

Úkol č. 4

Funkce a její derivace

• Nakreslete pod sebe 3 související grafy (stejné měřítko na ose nezávisle proměnné). V prvním nakreslete zvolenou funkci, ve druhém její derivaci, ve třetím její druhou derivaci. Popište co nejvíce, co umíte z funkcí vyčíst, např. kdy (tj. pro které hodnoty nezávisle proměnné) je ta která funkce např. rostoucí a proč - ukažte, jak se projevuje na navazujícím grafu ...

 

Z výše uvedeného řešení lze vidět souvislosti mezi třemi derivacemi funkce.

Derivace paraboly je v tomto případě rostoucí přímka a její derivací je potom neměnná (ani rostoucí ani klesající) přímka.

Úkol č. 3

Sklon funkce na intervalu a v bodě. Posun a otočení křivky. Extrém funkce a její derivace.

• Procvičte si dané pojmy, případně jiné související problémy.
• Jednou z možností je nakreslit pod sebe dva grafy (stejné měřítko na ose nezávisle proměnné). Do horního obrázku funkci (např. s extrémy, inflexními body apod.) a do spodního obrázku její derivaci. Pozor na souvislosti - zvýrazněte je, popište.
• Reagujte, prosím, na příspěvky svých kolegů, komentujte, vyjadřujte souhlas, pochybnosti, zdůvodňujte apod.

Z výše uvedeného řešení úkolu jde vidět souvislost s funkcí a její derivací.

Lze vidět, že rostoucí část s rostoucím sklonem je po derivaci rostoucí s rychlostí 2 a kdybychom fci g protáhli směrem dolů, viděli bychom, že derivace klesající části s rostoucím sklonem je rostoucí v záporných hodnotách.

Úkol č. 2

Lineární model 

• Lineární model budeme potkávat celý semestr. Připomeňte si co nejvíce o funkci: y = k.x + q.
• Zakreslete různá zadání, popište, kde a jak se projevuje hodnota k, jak hodnota q. Najděte např. funkci IS nebo LM a určete, jaký má sklon, jaký posun, zakreslete ji do osových souřadnic, popište co nejpečlivě, co všechno jste si uvědomili.
• Které ekonomické veličiny mohou způsobit posun některé z konkrétních ekonomických přímek (např. IS, LM, D, S aj.)? Zakreslete a popište.
• Které ekonomické veličiny mohou způsobit otočení některé z konkrétních ekonomických přímek (např. IS, LM, D, S aj.)? Zakreslete a popište.
• Materiál, který si vytvoříte při svém učení se, vložte zde elektronicky do fóra. Variant toho, co můžete vytvořit je dost pro každého!

 

Výše uvedené řešení úkolu ukazuje různé situace a dopady při změně hodnot q a hodnot k v lineárním modelu.

 

 Výše uvedené řešení úkolu ukazuje různé situace a příčiny, které mohou ovlivnit posun a otočení ekonomických přímek.

Tento úkol ukazuje důležitost hodnot otočení a posunu pro další studium. Nyní dokážeme určit při pouhém pohledu na funkci její rychlost a bod od kterého roste.

Úkol č.1

Záměna os může být osudná!

---

• Prolistujte svou ekonomickou knihu a najděte graf, ve kterém jsou nezávisle a závisle proměnná na opačných osách, než je v matematice obvyklé.
• Simulujte chybu, které byste se mohli záměnou dopustit.
• Pokud nenajdete nic jiného, zaměřte se na S-D model - nelineární! Pozor na "prohnutí" křivek - opticky je pokaždé jiné.
• Popište a zobrazte, např. naskenováním, kreslením v MS PowerPointu apod., situaci a svůj výsledek umístěte elektronicky do fóra prvního týdne.
• Reagujte na analogické příspěvky svých kolegů.
• Pokud máte neshody, nejasnosti, problémy, pište Zprávu (zde v Moodle) pedagogovi.

Další podoba úkolu:

• Nakreslete vedle sebe dva stejné grafy s lineární funkcí (do mřížky s měřítkem); jednou označte x - nezávisle proměnnou na vodorovnou osu, podruhé na svislou.
• Ke každé z funkcí napište rovnici: vlevo je u stejné funkce jiný předpis než vpravo (sledujte změny rychlostí; popište rychlosti a posuny ke grafům).

Další podoba úkolu:

• Nakreslete lineární funkci do grafu s nezávisle proměnnou x na vodorovné ose. Zapište její předpis.
• Nakreslete funkci s tímtež předpisem do vedlejšího obrázku s osou nezávisle proměnné x na svislé ose.

Řešení:

 

Z výše uvedeného řešení vyplývá, že v prvním případě obě funkce rostou, od -1 s rychlostí 2.

V druhém případě, kdy při změně os se rovnice přizpůsobí lze vidět velký rozdíl v obou grafech. U prvního grafu funkce roste od 3 s rychlostí 3 a u druhého grafu se změnila rovnice a tím pádem funkce roste od -1 s rychlostí 1/3.

Tento úkol názorně ukazuje, že může být záměna os opravdu osudná.