Úkol č. 19

Jsem se svým výkonem a se svým portfoliem výstupů spokojen(a)? Naučil(a) jsem se touto formou potřebné pro psaní SPP? Napište, prosím, kolik času jste průběžné práci věnovali, jak jste pracovali, co Vám vyhovovalo apod. Je něco, co si na dané formě Vašeho průběžného učení se ceníte? Myslíte, že Vám tvrdá práce v průběhu semestru čas nejen brala, ale v souhrnu také dala? Byli jste s probíranou látkou v kontaktu více než jindy? Dokázali jste se učit sami? A učili jste se? A naučili jste se? ... napište cokoliv dalšího.

Děkuji. DB.

Ano jsem se svým výkonem a portfoliem spokojená.

Ano díky těmto úkolům se mi na SPP lépe a jednodušeji učilo.

Na jednotlivých úkolech jsem pracovala různě dlouhé doby, ale v průměru přes hodinu na každém úkolu.

Velmi mi vyhovovala možnost podívat se na zpracování od ostatních studentů v případech, kdy jsem si s nějakým úkolem nevěděla rady.

Tvrdá práce pro mě měla přínos v tom, že jsem se nemusela tolik učit na SPP.

Materiálů v repository bylo k jednotlivým látkám dost. 

Je pravda, že mi navíc matematika pomohla v přípravě na zápočet makroekonomie B.

Mikulínová Markéta

Úkol č. 18

Dynamické modelování

1. Dynamické modelování v mikroekonomii:

A Procvičte si teorii na příkladech (s obrázky!)
- stačí pro nespojité změny
- se zpožděním na obou stranách
- pokaždé vedoucí ke konvergenci, resp. divergenci, celkem příklady.

B Látku si shrněte ve STRUKTUROVANÉM PŘEHLEDU - pro Vaše snadnější pochopení a zapamatování zákonitostí konvergence.

2. Dynamické modelování v makroekonomii - stačí jeden příklad s obrázkem.

Úkol č. 17

Funkce dvou proměnných slouží ekonomii - teorie užitku, teorie firmy, teorie investičního rozhodování

A Procvičení na příkladu teorie užitku

B Využití matematické abstrakce pro přechod od jednoho modelu k druhému - SYSTEMIZACE!

Tato část úkolu musí být bezpodmínečně zpracována velmi kvalitně. Vytvářejte k sobě příslušné položky, např. do tabulky - viz přednáška a cvičení. Nezapomeňte na grafická srovnání.

Úkol č. 16

Extrémní účinky fiskální a monetární politiky

Vypracujte si přehled extrémních účinků politik. Vždy řešte účinek pomocí limity.

Úkol č. 15

Velikost vytěsněné produkce vlivem fiskální resp. monetární politiky

Modelujte velikost vytěsněné produkce - početně a graficky. Tam, kde je to možné použijte obě metody výpočtu (1. pomocí bodů, 2. pomocí multiplikátorů), a tam, kde to možné není, použijte pouze metodu možnou.

• vlivem fiskální politiky
1. podoba fisk. pol.
2. podoba fisk. pol.
• vlivem monetární politiky

Každý student JEDEN příklad na fiskální politiku a JEDEN příklad na politiku monetární. Každý student bude mít příklad s vlastní volbou hodnot, tzn. každý příklad bude JINÝ. Pro KONTROLU Vám slouží co nejpřesněji nakreslený GRAF znázorňující zvolenou INTERVENCI.

FISKÁLNÍ POLITIKA

MONETÁRNÍ POLITIKA

Úkol č. 14

Sklony IS, LM pro konkrétní změny citlivosti.

Procvičujte příklady ze skript (elektronický text v repository) kapitola IS-LM, ale volte své vlastní zadání, tj. jiná čásla než jsou ve skriptech a než jsme řešili ve cvičeních!
KAŽDÝ STUDENT ALESPOŇ JEDEN Z NÁSLEDUJÍCÍCH 5 PŘÍKLADŮ - vždy početně i graficky, pokaždé odvozením přes AD, resp. L, ale také přímo z rovnic IS, resp. LM):
Každý odevzdaný příklad musí mít 4 části - pro přehlednost označte A, B, C, D - navzájem musí souhlasit, tj. nikdo nemůže mít chybný výsledek :-):

1. A Analytické odvození křivek z různými sklony + popis toho, co se stalo a čím to bylo zapřičiněno
2. B Grafické odvození křivek z různými sklony + popis toho, co se stalo a čím to bylo zapřičiněno + kontrola s předchozím
3. C Analytické vyjádření křivek s pouitím vzorců  + popis toho, co se stalo a čím to bylo zapřičiněno + kontrola s předchozím
4. D Grafické zakreslení výsledků z bodu C  + popis toho, co se stalo a čím to bylo zapřičiněno + kontrola s předchozím

Své příspěvky ve fórech TŘIĎTE do 4, resp. 5 skupin!

Řeště příklady s jinými čísly, než jsou ve skriptech nebo byla zvolena na cvičeních, tj. počítejte svůj příklad! ==> každý příklad bude jiný ( a od každého tam bude - aspoň jeden se 4 částmi :-) !)

1. úkol 2 ze skript: změna alfa (? sklon IS, multiplikační účinky) - volte změnu c
2. úkol 2 ze skript: změna alfa (? sklon IS, multiplikační účinky) - volte změnu t
3. úkol 3 ze skript: změna b (? sklon IS, multiplikační účinky)
4. úkol 5 ze skript: změna k (? sklon LM, multiplikační účinky)
5. úkol 5 ze skript: změna h (? sklon LM, multiplikační účinky)

Přehledně zapsat, přehledně zakreslit!!!
Nechť je četnost všech 4 příkladů srovnatelná, tj. dělej to, co je dosud ve fóru nejméně!

Úkol č. 7

Akumulace kapitálu

• Jak jsem si procvičil akumulaci kapitálu. Zejména v obrázcích zdůrazněte vztah mezi derivací a určitým integrálem - všechno viz animovaný výklad (repository).

Úkol č. 13

Sklony a posuny křivek IS, LM

Které veličiny ovlivní sklon, resp. posun křivky IS, resp. LM. Snažte se formulovat ekonomickou situaci, tu převeďte do mluvy lineárního modelu. Všechno kreslete, popisujte, zdůvodňujte.  

 

Úkol č. 12

Makroekonomická rovnováha v třísektorové ekonomice
Odvoďte multiplikační efekt ve tří sektorové ekonomice (případně s konkrétními čísly). Postupně můžete nejen "stavět nemocnici", ale také měnit velikost transferů, resp. autonomních daní, ba dokonce daňovou sazbu. Kdy se AD pouze posunuje, kdy se dokonce otáčí?
Multiplikační efekt vyznačte graficky.
DOPLNĚNÍ ÚKOLU (každý nechť má zápisky a hl. obrázky ke každé z těchto situací!): Analyzujte multiplikační efekty pro

1. změnu některých z autonomních výdajů (1-3 sektorová ekonomika)
2. změna mpc (zvýší se multiplikační efekt nebo sníží, proč?)
3. změna t (zvýší se multiplikační efekt nebo sníží, proč?)

Každou ze zakreslených situací si napište symbolicky (jako informaci, kterou stojí za to si zapamatovat), např. zvýšení mpc znamená strmější spotřební funkci, tzn. průsečíky pro rovnováhu jsou dále od sebe, tj. multiplikační efekt na důchod se pro větší mpc zesiluje - zapište v symbolech šipek, implikací atd.

Úkol č. 11

Elasticita, včetně paradoxu velké úrody atd.

Příklady k postupnému procvičování

• Zvol funkci rostoucí, resp. klesající a urči graficky jejich elasticity (viz přednáškové slidy).
• Zvol funkci nabídky (kvadratickou) a urči její elasticitu jako funkci, pak v jednom bodě - početně, graficky (viz příklad ze cvičení).
• Skupinový příklad pro změny diskrétní (pro poslední dodatečnou jednotku, viz Vaše ekonomické příklady, např. o snižování cen letenek apod.) - jen pro zájemce (nemusíte).
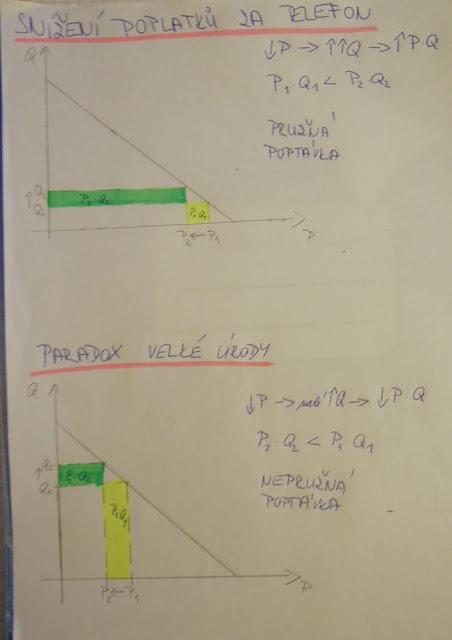
• Paradox velké úrody, resp. snížení poplatků za telefon (velmi často bývá na písemkách)!!!

Úkol č. 9

Vztah mezi veličinami průměrnými a mezními

 - Diskuze našeho týmu k tématu:

Příspěvky ve fóru:
 - Magda:

Ahoj týme,
můžete si zkusit tipnout, který z grafů mezních veličin je správně:-).

https://docs.google.com/file/d/0B90Ik4HFF4sMRTRMV29zay1TeVNYY1VoRkRIQWxhUQ/edit

 - Já:

Ahoj, nechybí ti tam ještě možnost d) ? :D
Když funkci y=(x+2)²+1 zderivuju tak mi vyjde y´=2x+4 - teda alespoň podle mě :) takže tím pádem mi vychází jiná funkce než tam máš nakreslenou (začíná od 4 a má rychlost 2)..
Možná si to všechno myslím špatně - dívala jsem se na to do repository a pochopila jsem to takhle..
Ale možná to všechno chápu špatně :)

  - Magda:

Ona vychází z 4 s rychlostí 2, jenom ty moje obrázky zachycují protažení toho grafu mezní veličiny na druhou stranu, takže by toi mělo být a). Myslím:-).

 - Já

Jo aha už to vidím.. Vůbec mi nedošlo jak vypadá na druhé straně a zmátlo mě, že tam nemáš to protnutí osy y ve 4 :) já jsem si to kreslila nějak takhle (viz níže uvedený obrázek) - dokreslila jsem tam i druhou stranu :-) tím pádem se to shoduje s odpovědí a)

Úkol č. 8

Maximalizace zisku

• Výpočtem hledejte maximální zisk pomocí dvou metod:
  
• MC = MR (ekonomické pravidlo)
• Hledání extrému funkce (využití diferenciálního počtu)
• a hledejte spojitosti obou výpočtů.
• Zakreslete pod sebe 3 související grafy a do nich VŠECHNY RELEVANTNÍ ÚDAJE A SOUVISLOSTI (POPIŠTE CO NEJVÍCE):
• TR, TC
• MR, MC
• zisk pi
• Hledejte pro funkce:
• TR = 11 300 Q - 22Q²
• TC = 4 Q³ - 16 Q² + 140 Q + 1780

• Pro nákresy určujte vrcholy, resp. konvexnost a konkávnost funkcí aj.

                                                                                                                                                                 

 Řešení: 

Z výše uvedeného můžeme vyčíst, že nejvyšší zisk je při Q=30 a to 219 620,- Kč.

Úkol č. 6

Hladká funkce

• Pochopte prostý pojem HLADKOST, pak jej dokážete vysvětlit exaktně. Cvičte si přesné vyjadřování, vše doplňujte vysvětlováním na obrázcích. Inspirací Vám může být studijní materiál z Repository s názvem Hladká funkce.

 V řešení tohoto úkolu se ověřovala hypotéza, která tvrdila, že je křivka hladká. Dále se ověřovalo nepotvrzení této hypotézy zjišťováním, zda je fce spojitá.

Úkol č. 5

Mezní sklon ke spotřebě

• Rozumím tomu, proč mezní sklon ke spotřebě nabývá hodnot mezi nulou a jedničkou, nebo jsem se tuto skutečnost jen naučil(a)? Popište své znalosti o tom, proč tomu tak je. Nemusíte všechno vymyslet sami, využijte dostupné zdroje - tím, že si informace vlastnoručně (a zejména "vlastnohlavně" :-)) zapíšete, mnohé si uvědomíte a pochopíte, také lépe zapamatujete. 
• Možná můžete začít tím, že vložíte odkaz na studijní materiál, který se tímto zabývá a je součástí tohoto kurzu - najdete jej v repository. Už jste jej našli? Vložte odkaz pro ostatní. Pak s ním pracujte, zapisujte si a některé své pěkné výstupy ukažte - zde prostřednictvím fóra - svým kolegům!

Z výše uvedeného můžeme vidět jednotlivé souvislosti mezi spotřební funkcí a mezním sklonem ke spotřebě. Lze pochopit, že mezní sklon ke spotřebě udává rychlost změn spotřební funkce při rostoucím důchodu.

Úkol č. 4

Funkce a její derivace

• Nakreslete pod sebe 3 související grafy (stejné měřítko na ose nezávisle proměnné). V prvním nakreslete zvolenou funkci, ve druhém její derivaci, ve třetím její druhou derivaci. Popište co nejvíce, co umíte z funkcí vyčíst, např. kdy (tj. pro které hodnoty nezávisle proměnné) je ta která funkce např. rostoucí a proč - ukažte, jak se projevuje na navazujícím grafu ...

 

Z výše uvedeného řešení lze vidět souvislosti mezi třemi derivacemi funkce.

Derivace paraboly je v tomto případě rostoucí přímka a její derivací je potom neměnná (ani rostoucí ani klesající) přímka.

Úkol č. 3

Sklon funkce na intervalu a v bodě. Posun a otočení křivky. Extrém funkce a její derivace.

• Procvičte si dané pojmy, případně jiné související problémy.
• Jednou z možností je nakreslit pod sebe dva grafy (stejné měřítko na ose nezávisle proměnné). Do horního obrázku funkci (např. s extrémy, inflexními body apod.) a do spodního obrázku její derivaci. Pozor na souvislosti - zvýrazněte je, popište.
• Reagujte, prosím, na příspěvky svých kolegů, komentujte, vyjadřujte souhlas, pochybnosti, zdůvodňujte apod.

Z výše uvedeného řešení úkolu jde vidět souvislost s funkcí a její derivací.

Lze vidět, že rostoucí část s rostoucím sklonem je po derivaci rostoucí s rychlostí 2 a kdybychom fci g protáhli směrem dolů, viděli bychom, že derivace klesající části s rostoucím sklonem je rostoucí v záporných hodnotách.

Úkol č. 2

Lineární model 

• Lineární model budeme potkávat celý semestr. Připomeňte si co nejvíce o funkci: y = k.x + q.
• Zakreslete různá zadání, popište, kde a jak se projevuje hodnota k, jak hodnota q. Najděte např. funkci IS nebo LM a určete, jaký má sklon, jaký posun, zakreslete ji do osových souřadnic, popište co nejpečlivě, co všechno jste si uvědomili.
• Které ekonomické veličiny mohou způsobit posun některé z konkrétních ekonomických přímek (např. IS, LM, D, S aj.)? Zakreslete a popište.
• Které ekonomické veličiny mohou způsobit otočení některé z konkrétních ekonomických přímek (např. IS, LM, D, S aj.)? Zakreslete a popište.
• Materiál, který si vytvoříte při svém učení se, vložte zde elektronicky do fóra. Variant toho, co můžete vytvořit je dost pro každého!

 

Výše uvedené řešení úkolu ukazuje různé situace a dopady při změně hodnot q a hodnot k v lineárním modelu.

 

 Výše uvedené řešení úkolu ukazuje různé situace a příčiny, které mohou ovlivnit posun a otočení ekonomických přímek.

Tento úkol ukazuje důležitost hodnot otočení a posunu pro další studium. Nyní dokážeme určit při pouhém pohledu na funkci její rychlost a bod od kterého roste.

Úkol č.1

Záměna os může být osudná!

---

• Prolistujte svou ekonomickou knihu a najděte graf, ve kterém jsou nezávisle a závisle proměnná na opačných osách, než je v matematice obvyklé.
• Simulujte chybu, které byste se mohli záměnou dopustit.
• Pokud nenajdete nic jiného, zaměřte se na S-D model - nelineární! Pozor na "prohnutí" křivek - opticky je pokaždé jiné.
• Popište a zobrazte, např. naskenováním, kreslením v MS PowerPointu apod., situaci a svůj výsledek umístěte elektronicky do fóra prvního týdne.
• Reagujte na analogické příspěvky svých kolegů.
• Pokud máte neshody, nejasnosti, problémy, pište Zprávu (zde v Moodle) pedagogovi.

Další podoba úkolu:

• Nakreslete vedle sebe dva stejné grafy s lineární funkcí (do mřížky s měřítkem); jednou označte x - nezávisle proměnnou na vodorovnou osu, podruhé na svislou.
• Ke každé z funkcí napište rovnici: vlevo je u stejné funkce jiný předpis než vpravo (sledujte změny rychlostí; popište rychlosti a posuny ke grafům).

Další podoba úkolu:

• Nakreslete lineární funkci do grafu s nezávisle proměnnou x na vodorovné ose. Zapište její předpis.
• Nakreslete funkci s tímtež předpisem do vedlejšího obrázku s osou nezávisle proměnné x na svislé ose.

Řešení:

 

Z výše uvedeného řešení vyplývá, že v prvním případě obě funkce rostou, od -1 s rychlostí 2.

V druhém případě, kdy při změně os se rovnice přizpůsobí lze vidět velký rozdíl v obou grafech. U prvního grafu funkce roste od 3 s rychlostí 3 a u druhého grafu se změnila rovnice a tím pádem funkce roste od -1 s rychlostí 1/3.

Tento úkol názorně ukazuje, že může být záměna os opravdu osudná.