Úkol č. 13

Sklony a posuny křivek IS, LM

Které veličiny ovlivní sklon, resp. posun křivky IS, resp. LM. Snažte se formulovat ekonomickou situaci, tu převeďte do mluvy lineárního modelu. Všechno kreslete, popisujte, zdůvodňujte.  

 

Úkol č. 12

Makroekonomická rovnováha v třísektorové ekonomice
Odvoďte multiplikační efekt ve tří sektorové ekonomice (případně s konkrétními čísly). Postupně můžete nejen "stavět nemocnici", ale také měnit velikost transferů, resp. autonomních daní, ba dokonce daňovou sazbu. Kdy se AD pouze posunuje, kdy se dokonce otáčí?
Multiplikační efekt vyznačte graficky.
DOPLNĚNÍ ÚKOLU (každý nechť má zápisky a hl. obrázky ke každé z těchto situací!): Analyzujte multiplikační efekty pro

1. změnu některých z autonomních výdajů (1-3 sektorová ekonomika)
2. změna mpc (zvýší se multiplikační efekt nebo sníží, proč?)
3. změna t (zvýší se multiplikační efekt nebo sníží, proč?)

Každou ze zakreslených situací si napište symbolicky (jako informaci, kterou stojí za to si zapamatovat), např. zvýšení mpc znamená strmější spotřební funkci, tzn. průsečíky pro rovnováhu jsou dále od sebe, tj. multiplikační efekt na důchod se pro větší mpc zesiluje - zapište v symbolech šipek, implikací atd.

Úkol č. 11

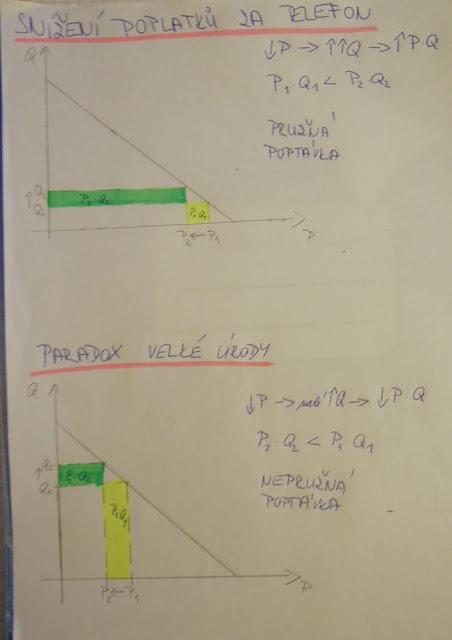
Elasticita, včetně paradoxu velké úrody atd.

Příklady k postupnému procvičování

• Zvol funkci rostoucí, resp. klesající a urči graficky jejich elasticity (viz přednáškové slidy).
• Zvol funkci nabídky (kvadratickou) a urči její elasticitu jako funkci, pak v jednom bodě - početně, graficky (viz příklad ze cvičení).
• Skupinový příklad pro změny diskrétní (pro poslední dodatečnou jednotku, viz Vaše ekonomické příklady, např. o snižování cen letenek apod.) - jen pro zájemce (nemusíte).
• Paradox velké úrody, resp. snížení poplatků za telefon (velmi často bývá na písemkách)!!!

Úkol č. 9

Vztah mezi veličinami průměrnými a mezními

 - Diskuze našeho týmu k tématu:

Příspěvky ve fóru:
 - Magda:

Ahoj týme,
můžete si zkusit tipnout, který z grafů mezních veličin je správně:-).

https://docs.google.com/file/d/0B90Ik4HFF4sMRTRMV29zay1TeVNYY1VoRkRIQWxhUQ/edit

 - Já:

Ahoj, nechybí ti tam ještě možnost d) ? :D
Když funkci y=(x+2)²+1 zderivuju tak mi vyjde y´=2x+4 - teda alespoň podle mě :) takže tím pádem mi vychází jiná funkce než tam máš nakreslenou (začíná od 4 a má rychlost 2)..
Možná si to všechno myslím špatně - dívala jsem se na to do repository a pochopila jsem to takhle..
Ale možná to všechno chápu špatně :)

  - Magda:

Ona vychází z 4 s rychlostí 2, jenom ty moje obrázky zachycují protažení toho grafu mezní veličiny na druhou stranu, takže by toi mělo být a). Myslím:-).

 - Já

Jo aha už to vidím.. Vůbec mi nedošlo jak vypadá na druhé straně a zmátlo mě, že tam nemáš to protnutí osy y ve 4 :) já jsem si to kreslila nějak takhle (viz níže uvedený obrázek) - dokreslila jsem tam i druhou stranu :-) tím pádem se to shoduje s odpovědí a)

Úkol č. 8

Maximalizace zisku

• Výpočtem hledejte maximální zisk pomocí dvou metod:
  
• MC = MR (ekonomické pravidlo)
• Hledání extrému funkce (využití diferenciálního počtu)
• a hledejte spojitosti obou výpočtů.
• Zakreslete pod sebe 3 související grafy a do nich VŠECHNY RELEVANTNÍ ÚDAJE A SOUVISLOSTI (POPIŠTE CO NEJVÍCE):
• TR, TC
• MR, MC
• zisk pi
• Hledejte pro funkce:
• TR = 11 300 Q - 22Q²
• TC = 4 Q³ - 16 Q² + 140 Q + 1780

• Pro nákresy určujte vrcholy, resp. konvexnost a konkávnost funkcí aj.

                                                                                                                                                                 

 Řešení: 

Z výše uvedeného můžeme vyčíst, že nejvyšší zisk je při Q=30 a to 219 620,- Kč.

Úkol č. 6

Hladká funkce

• Pochopte prostý pojem HLADKOST, pak jej dokážete vysvětlit exaktně. Cvičte si přesné vyjadřování, vše doplňujte vysvětlováním na obrázcích. Inspirací Vám může být studijní materiál z Repository s názvem Hladká funkce.

 V řešení tohoto úkolu se ověřovala hypotéza, která tvrdila, že je křivka hladká. Dále se ověřovalo nepotvrzení této hypotézy zjišťováním, zda je fce spojitá.

Úkol č. 5

Mezní sklon ke spotřebě

• Rozumím tomu, proč mezní sklon ke spotřebě nabývá hodnot mezi nulou a jedničkou, nebo jsem se tuto skutečnost jen naučil(a)? Popište své znalosti o tom, proč tomu tak je. Nemusíte všechno vymyslet sami, využijte dostupné zdroje - tím, že si informace vlastnoručně (a zejména "vlastnohlavně" :-)) zapíšete, mnohé si uvědomíte a pochopíte, také lépe zapamatujete. 
• Možná můžete začít tím, že vložíte odkaz na studijní materiál, který se tímto zabývá a je součástí tohoto kurzu - najdete jej v repository. Už jste jej našli? Vložte odkaz pro ostatní. Pak s ním pracujte, zapisujte si a některé své pěkné výstupy ukažte - zde prostřednictvím fóra - svým kolegům!

Z výše uvedeného můžeme vidět jednotlivé souvislosti mezi spotřební funkcí a mezním sklonem ke spotřebě. Lze pochopit, že mezní sklon ke spotřebě udává rychlost změn spotřební funkce při rostoucím důchodu.